L1 Lineare Optimierungsprobleme
Grafische Darstellung und Lösung
Bevor es im nächsten Kapitel an das algorithmische Lösungsverfahren geht, ist in diesem Abschnitt die grafische Darstellung und Lösung von Linearen Optimierungsproblemen Thema. Dieser Ansatz scheidet bei Problemen von realistischer Größe fast immer aus, da nur Probleme mit zwei Variablen darstell- und lösbar sind. Probleme mit drei Variablen lassen sich immerhin noch darstellen. Mit der grafischen Darstellung vor Augen lässt sich allerdings besser nachvollziehen, wie der Algorithmus funktioniert.
Das Koordinatensystem
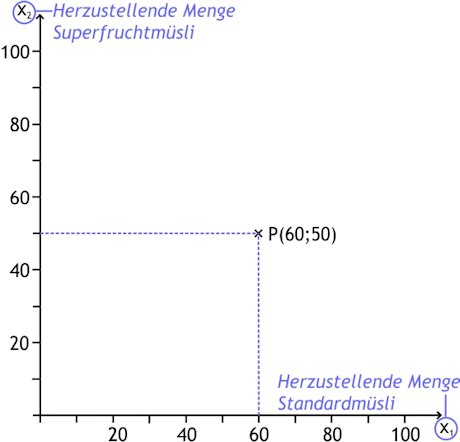
Zunächst wird ein Koordinatensystem gezeichnet. Auf der Abszisse wird die herzustellende Menge Standardmüsli, auf der Ordinate die herzustellende Menge Superfruchtmüsli abgetragen. Der Punkt P(60;50) bedeutet zum Beispiel, dass 60 kg Standardmüsli und 50 kg Superfruchtmüsli hergestellt werden.
Grenzlinie
Ecken
konvex
Darstellung der Nebenbedingungen
Nun werden die Nebenbedingungen eingezeichnet. Zu jeder Nebenbedingung gibt es eine Grenzlinie. Alle Punkte auf der einen Seite der Grenze erfüllen die Ungleichung. Diese Seite ist schattiert dargestellt. Auf der anderen Seite der Grenzlinie liegen die Punkte, die die Ungleichung nicht erfüllen. Die Grenze selbst ist zulässig, weil es sich um Kleiner-gleich-Nebenbedingungen handelt.
Da es lineare Nebenbedingungen sind, ist die Grenze immer eine Gerade.
Einzeichnen einer Nebenbedingung
Am Beispiel der Nebenbedingung für die Haferflocken:
0,8·x1+ 0,8·x2≤80
Um eine Gerade einzeichnen zu können, benötigt man zwei Punkte. Besonders einfach ist, wenn man dafür den Schnittpunkt mit der Abszisse und der Ordinate wählt.
Schnittpunkt mit Abszisse:
| 0,8·x1+ 0,8·0 =80 | //Hier „=“ Zeichen, da es sich um die Grenzlinie handelt // Am Schnittpunkt mit Abszisse ist x2=0 |
| 0,8·x1=80 | |
| x1 =100 | |
| P1(0;100) |
Und entsprechend für die Ordinate
0,8·0+ 0,8·x2=80
x2=100
P2(100;0)
Testen verschiedener Punkte
Zur Erinnerung, 80 kg Haferflocken sind vorhanden. Für je ein kg Standard- oder Superfruchtmüsli benötigt man 0,8 kg Haferflocken.

Punkt A:
Ist es mit den vorhandenen Haferflocken möglich, 40 kg Standardmüsli und 10 kg Superfruchtmüsli herzustellen?
Ja, der Punkt A(40|10) liegt auf der schattierten Seite der Grenze, d.h. es ist mögliche diese Mengen herzustellen.
Mathematisch bedeutet das, die Ungleichung
0,8·50+ 0,8·10 ≤80
48≤80
ist erfüllt! Wie sich nachrechnen lässt, es bleiben 80-48=32 kg Haferflocken übrig.
Punkt B:
Ist es möglich 40 kg Standard- und 60 kg Superfruchtmüsli mit den vorhandenen Haferflocken herzustellen?
Der Punkt B liegt genau auf der Grenzlinie! Es ist möglich diese Mengen herzustellen.
Die Ungleichung
0,8·40+ 0,8·60 ≤80
80≤80
ist erfüllt. Es bleiben keine Haferflocken übrig. Wie auch bei allen anderen Kombinationen, die auf der Grenzlinie liegen, werden alle Haferflocken aufgebraucht.
Punkt C:
Reichen die Haferflocken, um 70 kg bzw. 50 kg der Müslis herzustellen? Der Punkt C liegt auf der nichtschraffierten Seite der Grenzlinie. Es ist nicht möglich, diese Menge herzustellen.
Die Ungleichung
0,8·70+ 0,8·50 ≤80
96≤80
ist nicht erfüllt.
Es lässt sich nachrechnen, dass 80-96=-16 kg „übrig“ bleiben, mit anderen Worten gesagt, es fehlen 16 kg.
Die Nebenbedingungen in Gesamtheit
Auf diese Weise lassen sich auch die übrigen Nebenbedingungen einzeichnen. Damit eine Mengenkombination herstellbar ist, müssen alle Nebenbedingungen erfüllt sein. Die Lösungsmenge entspricht dem Bereich, in dem alle Nebenbedingungen und auch die Nichtnegativitätsbedingungen erfüllt sind.

An verschiedenen Stellen sind unterschiedliche Nebenbedingungen einschränkend. Der zulässige Bereich hat einige „Ecken“, an diesen Stellen sind zwei Nebenbedingungen einschränkend.
Noch eine Eigenschaft sei erwähnt, der zulässige Bereich ist konvex. Das bedeutet, wenn man zwei Punkte innerhalb oder auf den Grenzen des Bereichs miteinander verbindet, liegt die Verbindungslinie vollständig innerhalb dieses Bereichs. Das ist eine wichtige Eigenschaft, die nicht nur in diesem Beispiel, sondern bei Linearen Optimierungsproblemen immer gegeben ist.
Die Zielfunktion
Nun ist die spannende Frage, welcher Punkt im zulässigen Bereich der beste ist.
Vorüberlegungen
Auf dem Weg zur Beantwortung dieser Frage lässt sich die Zielfunktion für einen bestimmten Zielwert einzeichnen.
max z= 6·x1+ 8·x2
Zum Beispiel kann man sie, die Zahl ist willkürlich gewählt, für z=360 einzeichnen.
360= 6·x1+ 8·x2
Die Gerade zeigt alle Mengenkombinationen, auf denen ein Zielwert von 360 erreicht wird. Auf dem Abschnitt der Geraden der durch den Lösungsbereich führt bzw. ihn berührt, liegen die zulässigen Mengenkombinationen mit denen dieser Zielwert erreicht wird.
Um die Zielfunktion besser zu verstehen, noch einmal die Zielfunktion für einen anderen Zielwert, diesmal 480.
480= 6·x1+ 8·x2
Die Gerade verläuft parallel zu der Ersten. Auch sie hat Abschnitte im zulässigen Bereich. Wählt man allerdings z=840, erhält man eine Gerade, die ebenfalls parallel zu den anderen ist, die aber komplett außerhalb des zulässigen Bereichs verläuft. Es gibt mit den vorhandenen Vorräten keine Mengenkombination, mit der dieser Zielwert erreicht wird.

Vorgehen
Um den optimalen Punkt zu erreichen, empfiehlt es sich eine Gerade für einen beliebigen Zielwert einzuzeichnen und diese so parallel zu verschieben, dass sie möglichst weit oben-rechts ist und den zulässigen Bereich nur noch berührt. Die Werte x1 und x2 bei dem der optimale Zielwert erreicht wird, lassen sich an dem Punkt ablesen, an dem die Gerade den Lösungsraum berührt.
Beobachtung
Das Optimum muss immer auch an einem Eckpunkt erreicht werden! Führt die Gerade durch das Innere des Lösungsbereichs, lässt sie sich stets weiter nach rechts verschieben und ein höherer Zielwert erreichen.
Diese Feststellung lässt sich auch beweisen, was an dieser Stelle nicht getan wird. Sie gilt sinngemäß auch im höherdimensionalen Raum, das heißt, wenn es mehr als zwei oder drei Variablen gibt und das Problem nicht mehr grafisch dargestellt werden kann.
Der später vorgestellte Simplexalgorithmus konzentriert sich deswegen auch darauf, in den Ecken des zulässigen Bereichs zu suchen.


